归并排序图解
2015年03月10日 Algorithm

归并排序笔记，记录下来也希望可以帮助他人，尽可能说得明白。

归并排序是一种分治法的典型应用，就是将一个待排序的无序表不停的切割二部分，再对这二部分再切割成二部分，一直进行到每个单独的部分都只剩一个元素（一个元素就可以认为是这个元素是有序的，在代码上也就是使用递归，切分数组为N个小数组，直到每次小数组长度为1），这就是分治（递归）的出口，切割的部分只剩一个元素的时候，每个单独的元素当做一个有序表，开始合并每个切割的部分，每次合并，就相当于把二个有序表合并成一个有序表，上面是“拆分”开来，现在“合并”回去，直接到整个表都合并完成，这样这个无序表就变成了有序表。可能说不是很明白，还是像上次的快速排序，看图可能理解得更快一些。

下面有一个待排序的数组（无序表）：

有一个这样儿的无序数组（叫array），接下来一步一步演示用归并排序把这个无序数组按从小到大的顺序排列。

  1. 切分数组，以数组长度的中点为界将数组array切割为二部分，数组长度为11，中点为5，这样数组就被切分为array[0…5]和array[6-10]二部分：

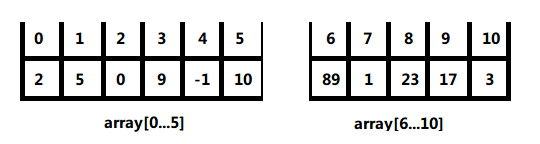
  2. 初切分出来的二个子数组长度都大于1，则对其左侧继续切割拆分，左侧与右侧运用相同的分治原则，现在图示只拿左侧部分进行归并演示（右侧与左侧的过程相同），左侧数组长度为6，中点为3，数组被切割为array[0…3]与array[4…5]

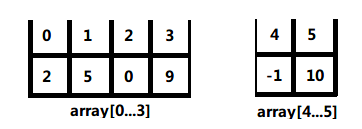
  3. 左侧依然长度大于1，继续对左侧切割拆分，子数组长度为4，中点为2，则数组拆分为array[0…2],array[3]

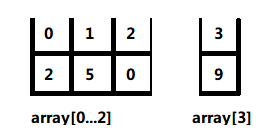
  4. 左侧数组长度仍然大于1，继续切分，子数组长度为3，中间为1，切分为array[0]与array[1..2]

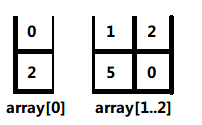
  5. 此时左侧子数组长度为1，只剩下一个元素（一个元素被认为是自有序的），左侧递归完成，开如4步中的右半部分拆分，右半部分数组长度为2，中点为1，数组拆分为array[1]与array[2]

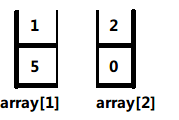
  6. 此时左边长度为1，不再递归切分，开始切分右边，右边长度也为1，也不再递归，那么这二个子数组开始合并，二个单独的子数组做排序归并处理（小在前，大在后），合并后的子数组为：

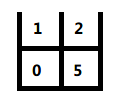
  7. 到此相当于第4步中右侧的子数组处理完毕开始返回，开始与第4步中左侧的子数组合并处理：

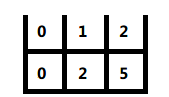
  8. 到此相当于第3步的左侧归并完毕，开始对右侧进行切分，右侧的子数组长度为1，不再进行拆分，直接开始与第7步中刚刚归并处理完的子数组继续归并：

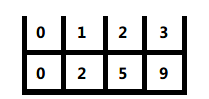
  9. 到此相当于第2步的左侧都归并处理完毕，开始对右侧进行切分处理。右侧长度为2，中间为1，数组为array[4]与array[5]

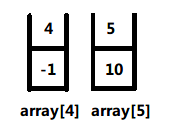
  10. 再对左侧进行切分，左侧子数组长度为1，不再递归，对右侧进行切分，右侧长度也为1，不再递归切分，二个子数组开始归并处理：

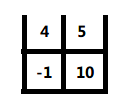
  11. 到此相当于第2步的右侧归并处理完毕，开始与左侧刚才已归并处理好的子数组进行归并处理:

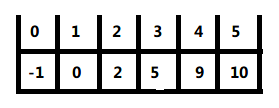
  12. 进行到这一步，就已经对第1步的左侧完全合并处理完成，开始对右侧进行切分，右侧也与刚才图示的左侧的切分过程完全相同，切分到子数组长度为1的时候，开始对子数组一路进行归并处理，直到像11步这样对右侧完全归并处理完成，右侧归并完成就是(省略具体切分过程，与上述左侧切分过程完全相同)：

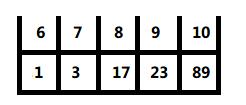
  13. 到这里，第1步的右侧归并完成，开始与左侧已经归并处理完成的子数组进行最终的归并处理，最后就得到了一个排好序的数组：

这样儿就是一个完整的归并排序的过程。如果有错误请您指出，非常感谢_。下面是代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include <stdio.h>

void merge_sorted_array(int *array1, int array1_len,
        int *array2, int array2_len)
{
    int merge_array[array1_len + array2_len];
    int arr1_loc = 0;
    int arr2_loc = 0;
    int merge_arr_loc = 0;

    //二个数组从开始比较，小的放到数组中
    while (arr1_loc < array1_len && arr2_loc < array2_len)
    {
        if (array1[arr1_loc] <= array2[arr2_loc])
        {
            merge_array[merge_arr_loc++] = array1[arr1_loc++];
        }
        else
        {
            merge_array[merge_arr_loc++] = array2[arr2_loc++];
        }
    }
    //数组中有剩余，则全部加入到合并数组中
    while (arr1_loc < array1_len)
    {
        merge_array[merge_arr_loc++] = array1[arr1_loc++];
    }
    while (arr2_loc < array2_len)
    {
        merge_array[merge_arr_loc++] = array2[arr2_loc++];
    }
    //最后把辅助数组，覆盖到原数组
    for (int i = 0; i < merge_arr_loc; i++)
    {
        array1[i] = merge_array[i];
    }
}

void merge_sort(int *array, int size)
{
    if (size < 2)
    {
        return ;
    }
    else
    {
        int *pre_part = array;
        int *next_part = array + size / 2;

        int pre_len = size / 2;
        int next_len = size - pre_len;

        merge_sort(pre_part, pre_len);
        merge_sort(next_part, next_len);

        merge_sorted_array(pre_part, pre_len, next_part, next_len);
    }
}

int main(int argc, char *argv[])
{
    int array1[11] = {2, 5, 0, 9, -1, 10, 89, 1, 23, 17, 3};

    merge_sort(array1, 11);
    for (int i = 0; i < 11; i++)
    {
        printf("%d\n", array1[i]);
    }

    return 0;
}